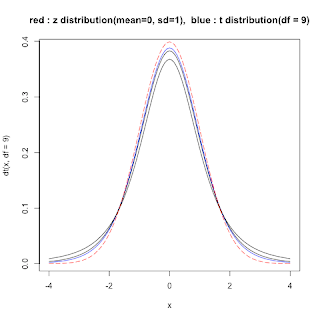
#Rを用いて、自由度dfが大きいときのt分布がz分布(平均値0, 標準偏差1の正規分布)に
#近似が可能なことを視覚的に理解する。
png("z-t.png")
curve(dt(x,df=9), from = -4, to = 4,col = "blue", main="red : z distribution(mean=0, sd=1), blue : t distribution(df = 9)")
curve(dt(x,df=6), from = -4, to = 4, add=T)
curve(dt(x,df=3), from = -4, to = 4, add=T)
curve(dnorm(x, mean=0, sd=1), add=T, col = "red", lty=5)
dev.off()
#######数式のソースファイル#############
% t.tex
\documentclass[a4j]{jarticle}
\usepackage{amsmath}
\begin{document}
これまでは母分散$\sigma^2$が既知である場合の標本平均$\bar X$について考えてきました。
しかし、実際の場面ではこのようなことは起こりえない。
従って母分散が不明の場合に母平均の区間推定を行う場合は、
$\sigma^2$の点推定値である$s^2$を用いた理論構築が必要となる。
正規分布$N(\mu, \sigma^2)$からのサンプルの標本平均は正規分布$N(\mu, \sigma^2/n)$に従い、その標準化したものは、
\begin{eqnarray*}
Z = \frac{\bar X - \mu}{\sqrt{\sigma^2/n}}
\end{eqnarray*}
である。$Z$は$N(0,1)$の標準正規分布に従う。ここで$Z$の形式を参考にして、以下のようにして統計量$t$を新たに定義する。\\
\begin{eqnarray*}
t = \frac{\bar X - \mu}{\sqrt{s^2/n}}
\end{eqnarray*}
この統計量$t$をスチューデントの$t$統計量 Student's t-statisticと呼ぶ。
$t$統計量は、自由堂$n-1$の$t$分布$t(n - 1)$に従う。
信頼係数$1 - \alpha$が与えられたならば、
\begin{eqnarray*}
P(- t_{n-1}(\frac{\alpha}{2}) \leq t \leq t_{n-1}(\frac{\alpha}{2})) = 1 - \alpha \\
P(- t_{n-1}(\frac{\alpha}{2}) \leq \frac{\bar X - \mu}{\sqrt{\frac{s^2}{n}}} \leq t_{n-1}(\frac{\alpha}{2})) = 1 - \alpha \\
\end{eqnarray*}
左辺内の括弧内を$\mu$について解くと、
\begin{eqnarray*}
P(\bar X - t_{n-1}(\frac{\alpha}{2}) \cdot \sqrt{\frac{s^2}{n}} \leq \mu \leq \bar X + t_{n-1}(\frac{\alpha}{2}) \cdot \sqrt{\frac{s^2}{n}} ) = 1 - \alpha
\end{eqnarray*}
従って、母平均$\mu$の信頼係数$1 - \alpha$の信頼区間は
\begin{eqnarray*}
[\bar X - t_{n-1}(\frac{\alpha}{2}) \cdot \sqrt{\frac{s^2}{n}} \leq \mu \leq \bar X + t_{n-1}(\frac{\alpha}{2}) \cdot \sqrt{\frac{s^2}{n}}]
\end{eqnarray*}
となる。\\
\\
【例】製品の精度・強度(河田、丸山、鍋谷) 座金の製造工場において、ある日作られた座金の中から、100個を抽出してその厚さを測定したところ、
$\bar X = 2.346, s=0.047(mm)$であった。母平均$\mu$の信頼係数$90\%$の信頼区間を求めよ。\\
サンプル数が十分に多いため、t分布は標準正規分布に近似できるので、
\begin{eqnarray*}
t_0.05(100 - 1) \sim Z_0.05 = 1.645
\end{eqnarray*}
となる。したがって、$\mu$の信頼区間は
\begin{eqnarray*}
2.346\pm 1.645 \cdot \sqrt{0.047^2 / 100}
\end{eqnarray*}
となり、$[2.338,2.354]$となる。
\\【参考文献】\\
東京大学教養部統計学教室(1991) 『統計学入門』 東京大学出版 201,202, 226pp.\\
松原望(2007)『入門 統計解析 医学・自然科学編』東京図書 102 - 104pp.\\
馬場敬之 久池井茂『確率統計』マセマ 171,172pp
\pagestyle{empty}
\end{document}
###########ここまで#############